Question:
A particle is moving along the $x$-axis with its coordinate with time ' $t$ ' given by $x(t)=10+8 t-3 t^{2}$. Another particle is moving along the $y$-axis with its coordinate as a function of time given by $y(t)=5-8 t^{3}$. At $t=1 \mathrm{~s}$, the speed of the second particle as measured in the frame of the first particle is given as $\sqrt{v}$. Then $v($ in $\mathrm{m} / \mathrm{s})$ is________
Solution:
$(580)$
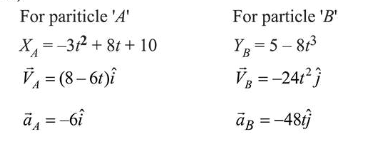
At $t=1 \mathrm{sec}$
$\vec{V}_{A}=(8-6 t) \hat{i}=2 \hat{i}$ and $\vec{v}_{B}=-24 \hat{j}$
$\therefore \vec{V}_{B / A}=-\vec{v}_{A}+\vec{v}_{B}=-2 \hat{i}-24 \hat{j}$
$\therefore \quad$ Speed of $B$ w.r.t. $A, \sqrt{v}=\sqrt{2^{2}+24^{2}}$
$=\sqrt{4+576}=\sqrt{580}$
$\therefore v=580(\mathrm{~m} / \mathrm{s})$
