Question:
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
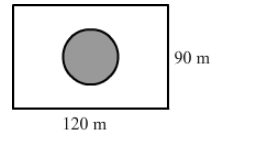
Solution:
Area of the rectangle $=l \times b$
$=120 \times 90$
$=10800$ sq. $\mathrm{m}$
Area of the park excluding the lawn = 2950 m2
Area of the circular lawn = Area of the park
$=10800-2950$
$=7850 \mathrm{~m}^{2}$
Area of the circular lawn $=\pi r^{2}$
$\Rightarrow 7850=\frac{22}{7} \times r^{2}$
$\Rightarrow \frac{7850 \times 7}{22}=r^{2}$
$\Rightarrow r^{2}=2497.72$
$\Rightarrow r=49.97$
Or,
$r \approx 50 \mathrm{~m}$
Thus, the radius of the circular lawn is 50 m.
