A parallel plate capacitor is made of two square plates of side ' $a$ ', separated by a distance $d(d<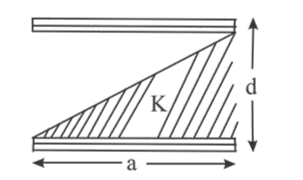
Correct Option: , 2
(2)
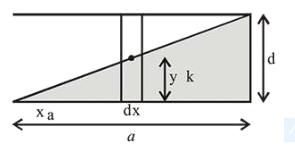
From figure, $\frac{\mathrm{y}}{\mathrm{x}}=\frac{\mathrm{d}}{\mathrm{a}} \Rightarrow \mathrm{y}=\frac{\mathrm{d}}{\mathrm{a}} \mathrm{x}$
$\mathrm{dy}=\frac{\mathrm{d}}{\mathrm{a}}(\mathrm{dx}) \Rightarrow \frac{1}{\mathrm{dc}}=\frac{\mathrm{y}}{\mathrm{K} \varepsilon_{0} \mathrm{adx}}+\frac{(\mathrm{d}-\mathrm{y})}{\varepsilon_{0} \mathrm{adx}}$
$\frac{1}{d c}=\frac{y}{\varepsilon_{0} a b x}\left(\frac{y}{k}+d-y\right)$
$\int \mathrm{dc}=\int \frac{\varepsilon_{0} \mathrm{adx}}{\frac{\mathrm{y}}{\mathrm{k}}+\mathrm{d}-\mathrm{y}}$
or, $c=\varepsilon_{0} a \cdot \frac{a}{d} \int_{0}^{d} \frac{d y}{d+y\left(\frac{1}{k}-1\right)}$
$=\frac{\varepsilon_{0} \mathrm{a}^{2}}{\left(\frac{1}{\mathrm{k}}-1\right) \mathrm{d}}\left[\ell \mathrm{n}\left(\mathrm{d}+\mathrm{y}\left(\frac{1}{\mathrm{k}}-1\right)\right)\right]_{0}^{\mathrm{d}}$
$=\frac{\mathrm{k} \in_{0} \mathrm{a}^{2}}{(1-\mathrm{k}) \mathrm{d}} \ell \mathrm{n}\left(\frac{\mathrm{d}+\mathrm{d}\left(\frac{1}{\mathrm{k}}-1\right)}{\mathrm{d}}\right)$
$=\frac{\mathrm{k} \in_{0} \mathrm{a}^{2}}{(1-\mathrm{k}) \mathrm{d}} \ell \mathrm{n}\left(\frac{1}{\mathrm{k}}\right)=\frac{\mathrm{k} \in_{0} \mathrm{a}^{2} \ell \mathrm{nk}}{(\mathrm{k}-1) \mathrm{d}}$
