A parallel plate capacitor has plate area $100 \mathrm{~m}^{2}$ and plate separation of $10 \mathrm{~m}$. The space between the plates is filled up to a thickness 5 $\mathrm{m}$ with a material of dielectric constant of 10 . The resultant capacitance of the system is ' $x^{\prime} \mathrm{pF}$. The value of $\varepsilon_{0}=8.85 \times 10^{-12} \mathrm{~F} . \mathrm{m}^{-1}$.
The value of ' $x$ ' to the nearest integer is__________.
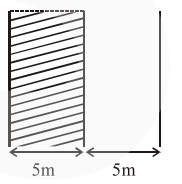
$A=100 \mathrm{~m}^{2}$
Using $\mathrm{C}=\frac{\mathrm{k} \in_{0} \mathrm{~A}}{\mathrm{~d}}$
$\mathrm{C}_{1}=\frac{10 \in_{0}(100)}{5}$
$=200 \in_{0}$
$\mathrm{C}_{2}=\frac{\epsilon_{0}(100)}{5}=20 \epsilon_{0}$
$C_{1} \& C_{2}$ are in series so $C_{\text {eqv }}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}$
$=\frac{4000 \epsilon_{0}}{220}$
$=160.9 \times 10^{-12} \simeq 161 \mathrm{pF}$
