A parallel plate capacitor with plate area 'A' and distance of separation 'd' is filled with a dielectric. What is the capacity of the capacitor when permittivity of the dielectric varies as :
$\varepsilon(x)=\varepsilon_{0}+k x$, for $\left(0 $\varepsilon(x)=\varepsilon_{0}+k(d-x)$, for $\left(\frac{d}{2} \leq x \leq d\right)$
Correct Option: , 2
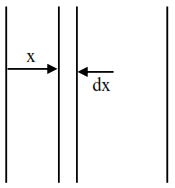
Taking an element of width $\mathrm{dx}$ at a distance
$\mathrm{x}(\mathrm{x}<\mathrm{d} / 2)$ from left plate
$\mathrm{dc}=\frac{\left(\varepsilon_{0}+\mathrm{kx}\right) \mathrm{A}}{\mathrm{dx}}$
Capacitance of half of the capacitor
$\frac{1}{\mathrm{C}}=\int_{0}^{\mathrm{d} / 2} \frac{1}{\mathrm{dc}}=\frac{1}{\mathrm{~A}} \int_{0}^{\mathrm{d} / 2} \frac{\mathrm{dx}}{\varepsilon_{0}+\mathrm{kx}}$
$\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{kA}} \ln \left(\frac{\varepsilon_{0}+\mathrm{kd} / 2}{\varepsilon_{0}}\right)$
Capacitance of second half will be same
$\mathrm{C}_{\mathrm{cq}}=\frac{\mathrm{C}}{2}=\frac{\mathrm{kA}}{2 \ln \left(\frac{2 \varepsilon_{0}+\mathrm{kd}}{2 \varepsilon_{0}}\right)}$
