A parabolic reflector is 5 cm deep and its diameter is 20 cm.

Given: Parabolic reflector is 5 cm deep & its diameter is 20 cm

Need to find: Distance of its focus from the vertex.

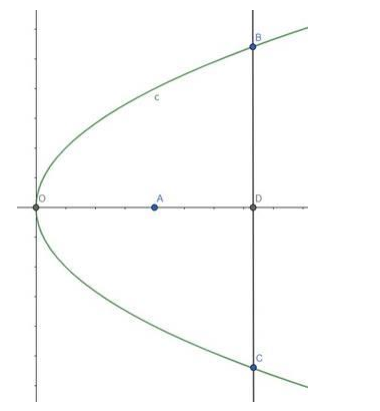
Reflector is $5 \mathrm{~cm}$ deep, i.e., $O D=5 \mathrm{~cm}$

Diameter of the mirror is $20 \mathrm{com}$, i.e., $B C=20 \mathrm{~cm}$

Let, the equation of the parabola is $y^{2}=4 a x$, where a is the distance of the focus from the vertex.

The $x$-coordinate of the points $B$ and $C$ is 5 .

$\mathrm{D}$ is the middle point of $\mathrm{BC}$ which is upon the $\mathrm{x}$-axis.

So, we can say that $B D=C D=10 \mathrm{~cm}$.

So, the coordinate of the point $B$ is $(5,10)$

Putting the values of the equation,

$y^{2}=4 a x$

$\Rightarrow 100=4 a \times 5$

$\Rightarrow 20 a=100$

$\Rightarrow a=5$

That means, the focus is 5 cm far from the vertex.