Question:
A modern grand-prix racing car of mass $m$ is travelling on a flat track in a circular arc of radius $R$ with a speed $v$. If the coefficient of static friction between the tyres and the track is $\mu_{\mathrm{s}}$, then the magnitude of negative lift $\mathrm{F}_{\mathrm{L}}$ acting downwards on the car is :
(Assume forces on the four tyres are identical and $g=$ acceleration due to gravity)
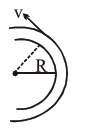
Correct Option: , 2
Solution:
$\mu_{\mathrm{s}} \mathrm{N}=\frac{\mathrm{mv}^{2}}{\mathrm{R}}$
$\mathrm{N}=\frac{\mathrm{mv}^{2}}{\mu_{\mathrm{s}} \mathrm{R}}=\mathrm{mg}+\mathrm{F}_{\mathrm{L}}$
$\mathrm{F}_{\mathrm{L}}=\frac{\mathrm{mv}^{2}}{\mu_{\mathrm{s}} \mathrm{R}}-\mathrm{mg}$
