A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of canvas used in making the tent, if the breadth of the canvas is 1.5 m.
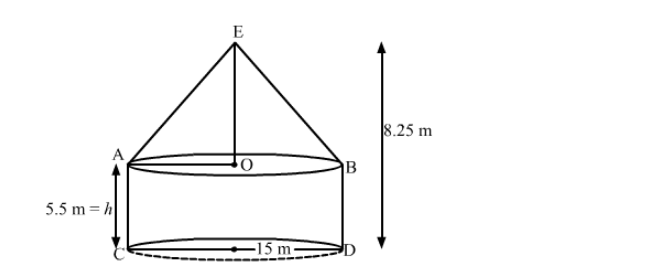
We have,
the radii of bases of the cone and cylinder, r = 15 m,
the height of the cylinder, h = 5.5 m,
the height of the tent = 8.25 m
Also, the height of the cone, $H=8.25-5.5=2.75 \mathrm{~m}$
The slant height of the cone, $l=\sqrt{r^{2}+H^{2}}$
$=\sqrt{15^{2}+2.75^{2}}$
$=\sqrt{225+7.5625}$
$=\sqrt{232.5625}$
$=15.25 \mathrm{~m}$
The area of the canvas used in making the tent $=$ CSA of cylinder $+$ CSA of cone
$=2 \pi r h+\pi r l$
$=\pi r(2 h+l)$
$=\frac{22}{7} \times 15(2 \times 5.5+15.25)$
$=\frac{22}{7} \times 15(11+15.25)$
$=\frac{22}{7} \times 15 \times 26.25$
$=1237.5 \mathrm{~m}^{2}$
As, the width of the canvas = 1.5 m
So, the length of the canvas $=\frac{237.5}{1.5}=825 \mathrm{~m}$
Hence, the length of the tent used for making the tent is 825 m.
