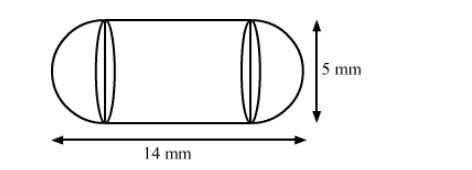
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends.

We have,

the total height of the capsule $=14 \mathrm{~mm}$ and

the radius of the capsule, $r=\frac{5}{2} \mathrm{~mm}$

Also, the height of the cylinder, $h=14-\left(2 \times \frac{5}{2}\right)=14-5=9 \mathrm{~mm}$

Now, the surface area of the capsule = CSA of the cylinder $+2 \times$ CSA of a hemisphere

$=2 \pi r h+2 \times 2 \pi r^{2}$

$=2 \pi r(h+2 r)$

$=2 \times \frac{22}{7} \times \frac{5}{2} \times\left(9+2 \times \frac{5}{2}\right)$

$=\frac{22}{7} \times 5 \times(9+5)$

$=\frac{22}{7} \times 5 \times 14$

$=220 \mathrm{~mm}^{2}$

So, the surface area of the medicine capsule is 220 mm2.