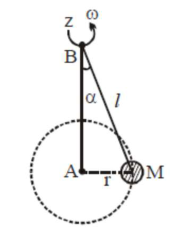
A mass $M$ hangs on a massless rod of length $l$ which rotates at a constant angular frequency. The mass $\mathrm{M}$ moves with steady speed in a circular path of constant radius. Assume that the system is in steady circular motion with constant angular velocity $\omega$. The angular momentum of $\mathrm{M}$ about point $\mathrm{A}$ is $\mathrm{L}_{\mathrm{A}}$ which lies in the positive $z$ direction and the angular momentum of $\mathrm{M}$ about $\mathrm{B}$ is $\mathrm{L}_{\mathrm{B}}$. The correct statement for this system is :
Correct Option: , 4
(4)
We know, $\overrightarrow{\mathrm{L}}=\mathrm{m}(\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{v}})$\
Now with respect to A, we always get direction
of $\overrightarrow{\mathrm{L}}$ along tve z-axis and also constant magnitude as mvr. But with respect
to $\mathrm{B}$, we get constant magnitude but continuously changing direction.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.