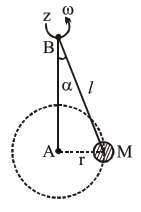
A mass $M$ hangs on a massless rod of length $l$ which rotates at a constant angular frequency. The mass $M$ moves with steady speed in a circular path of constant radius. Assume that the system is in steady circular motion with constant angular velocity $\omega$. The angular momentum of $M$ about point $A$ is $L_{A}$ which lies in the positive $z$ direction and the angular momentum of $M$ about $B$ is $L_{B}$. The correct statement for this system is :
Correct Option: , 4
We know, $\overrightarrow{\mathrm{L}}=\mathrm{m}(\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{V}})$
Now with respect to $\mathrm{A}$, we always get direction of $\overrightarrow{\mathrm{L}}$ along +ve z-axis and also constant magnitude as mvr. But with respect to $B$, we get constant magnitude but continuously changing direction.
