A man on the deck of a ship, 16 m above water level observes that the angles of elevation and depression respectively of the top and bottom of a cliff are 60° and 30°.

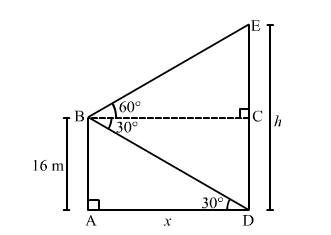
Let $A B$ be the deck of the ship above the water level and $D E$ be the cliff.

Now,

$A B=16 \mathrm{~m}$ such that $C D=16 \mathrm{~m}$ and $\angle B D A=30^{\circ}$ and $\angle E B C=60^{\circ}$.

If $A D=x \mathrm{~m}$ and $D E=h \mathrm{~m}$, then $C E=(h-16) \mathrm{m}$.

In the right $\triangle B A D$, we have:

$\frac{A B}{A D}=\tan 30^{\circ}=\frac{1}{\sqrt{3}}$

$\Rightarrow \frac{16}{x}=\frac{1}{\sqrt{3}}$

$\Rightarrow x=16 \sqrt{3}=27.68 \mathrm{~m}$

In the right $\Delta E B C$, we have:

$\frac{E C}{B C}=\tan 60^{\circ}=\sqrt{3}$

$\Rightarrow \frac{(h-16)}{x}=\sqrt{3}$

$\Rightarrow h-16=x \sqrt{3}$

$\Rightarrow h-16=16 \sqrt{3} \times \sqrt{3}=48 \quad[\because x=16 \sqrt{3}]$

$\Rightarrow h=48+16=64 \mathrm{~m}$

$\therefore$ Distance of the cliff from the deck of the ship $=A D=x=27.68 \mathrm{~m}$

And,

Height of the cliff $=D E=h=64 \mathrm{~m}$