A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed.

Suppose AB be the tower of height h meters. Let C be the initial position of the car and let after 12 minutes the car be at D. It is given that the angles of depression at C and D are 30º  and 45º respectively.
Let the speed of the car be v meter per minute. Then,
CD = distance travelled by the car in 12 minutes
CD = 12v meters

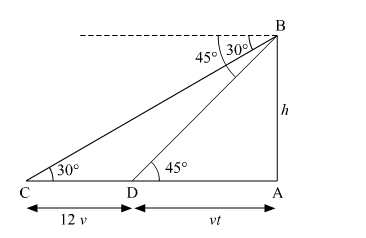
Suppose the car takes t minutes to reach the tower AB from D. Then DA = vt meters.

In $\Delta$ DAB, we have

$\tan 45^{\circ}=\frac{\mathrm{AB}}{\mathrm{AD}}$

$\Rightarrow 1=\frac{h}{v t}$

$\Rightarrow h=v t \quad \ldots .(i)$

In $\Delta$ CAB, we have

$\tan 30^{\circ}=\frac{\mathrm{AB}}{\mathrm{AC}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{v t+12 v}$

$\Rightarrow \sqrt{3} h=v t+12 v \quad \ldots .(i i)$

Substituting the value of h from equation (i) in equation (ii), we get

$\Rightarrow \sqrt{3} t=t+12$

$\Rightarrow t=\frac{12}{\sqrt{3}-1}=\frac{12}{(\sqrt{3}-1)} \times \frac{(\sqrt{3}+1)}{(\sqrt{3}+1)}=6(\sqrt{3}+1) \min$