A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the light house from 60° to 30°.

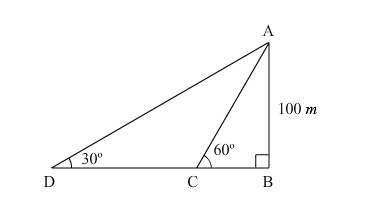
Let AB be the light house. Suppose C and D be the two positions of the boat.

Here, AB = 100 m.

Let the speed of the boat be v m/min.

So,

CD = v m/min × 2 min = 2v m          [Distance = Speed × Time]

In right ∆ABC,

$\tan 60^{\circ}=\frac{\mathrm{AB}}{\mathrm{BC}}$

$\Rightarrow \sqrt{3}=\frac{100 \mathrm{~m}}{B C}$

$\Rightarrow \mathrm{BC}=\frac{100}{\sqrt{3}}=\frac{100 \sqrt{3}}{3} \mathrm{~m} \quad \ldots . .(1)$

In right ∆ABD,

$\tan 30^{\circ}=\frac{\mathrm{AB}}{\mathrm{BD}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{100 \mathrm{~m}}{\mathrm{BC}+\mathrm{CD}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{100}{\frac{100 \sqrt{3}}{3}+2 v} \quad[$ From $(1)]$

$\Rightarrow 2 v+\frac{100 \sqrt{3}}{3}=100 \sqrt{3}$

$\Rightarrow 2 v=100 \sqrt{3}-\frac{100 \sqrt{3}}{3}$

$\Rightarrow 2 v=100 \sqrt{3}\left(1-\frac{1}{3}\right)$

$\Rightarrow 2 v=100 \sqrt{3} \times \frac{2}{3}$

$\Rightarrow v=\frac{100 \times 1.732}{3}=57.73 \mathrm{~m} / \mathrm{min}$

Thus, the speed boat is 57.73 m/min.