A ladder of length 6 metres makes an angle of 45° with the floor while leaning against one wall of a room.

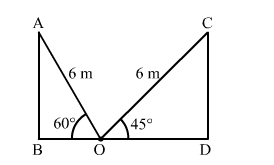
Let AB and CD be the two opposite walls of the room and the foot of the ladder be fixed at the point O on the ground.

We have,

$\mathrm{AO}=\mathrm{CO}=6 \mathrm{~m}, \angle \mathrm{AOB}=60^{\circ}$ and $\angle \mathrm{COD}=45^{\circ}$

In $\Delta \mathrm{ABO}$

$\cos 60^{\circ}=\frac{\mathrm{BO}}{\mathrm{AO}}$

$\Rightarrow \frac{1}{2}=\frac{\mathrm{BO}}{6}$

$\Rightarrow \mathrm{BO}=\frac{6}{2}$

$\Rightarrow \mathrm{BO}=3 \mathrm{~m}$

Also, in $\Delta \mathrm{CDO}$,

$\cos 45^{\circ}=\frac{\mathrm{DO}}{\mathrm{CO}}$

$\Rightarrow \frac{1}{\sqrt{2}}=\frac{\text { DO }}{6}$

$\Rightarrow$ DO $=\frac{6}{\sqrt{2}}$

$\Rightarrow$ DO $=\frac{6}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}$

$\Rightarrow$ DO $=\frac{6 \sqrt{2}}{2}$

$\Rightarrow$ DO $=3 \sqrt{2} \mathrm{~m}$

Now, the distance between two walls of the room $=\mathrm{BD}$

$=\mathrm{BO}+\mathrm{DO}$

$=3+3 \sqrt{2}$

$=3(1+\sqrt{2})$

$=3(1+1.414)$

$=3(2.414)$

$=7.242$

$\approx 7.24 \mathrm{~m}$

So, the distance between two walls of the room is 7.24 m.