A ladder 10 m long reaches the window of a house 8 m above the ground.

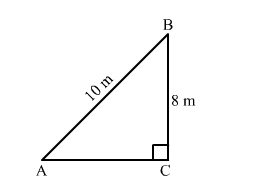
Let AB be a ladder and B is the window at 8 m above the ground C.
Now, In right triangle ABC
By using Pythagoras theorem, we have

$\mathrm{AB}^{2}=\mathrm{BC}^{2}+\mathrm{CA}^{2}$

$\Rightarrow 10^{2}=8^{2}+\mathrm{CA}^{2}$

$\Rightarrow \mathrm{CA}^{2}=100-64$

$\Rightarrow \mathrm{CA}^{2}=36$

$\Rightarrow \mathrm{CA}=6 \mathrm{~m}$

Hence, the distance of the foot of the ladder from the base of the wall is 6 m.