A kit is flying at a height of 75 metres from the ground level,

Let AC be the string of length h m and C be the point, makes an angle of 60° and the kite is flying at the height of 75 m from the ground level.

In a triangle, given that height of kite is AB = 75 m and angle C = 60°

Now we have to find the length of string.

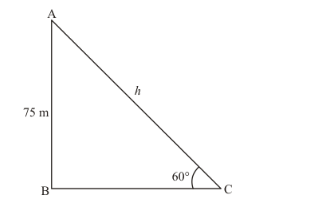
So we use trigonometric ratios.

In a triangle,

$\Rightarrow \quad \sin C=\frac{A B}{A C}$

$\Rightarrow \quad \sin 60^{\circ}=\frac{75}{h}$

$\Rightarrow \quad \frac{\sqrt{3}}{2}=\frac{75}{h}$

$\Rightarrow \quad h=\frac{150}{\sqrt{3}}$

Therefore h = 86.6

Hence length of string is  meters.