Question:
A horse is placed for grazing inside a rectangular field 70 m by 52 m. It is tethered to one corner by a rope 21 m long. On how much area can it graze? How much area is left ungrazed?
Solution:
Radius of the quadrant of the circle = 21 m
The shaded portion shows the part of the field the horse can graze.
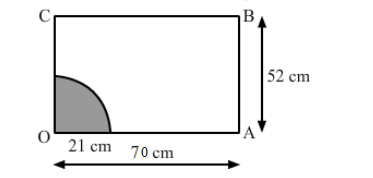
Area of the grazed field = Area of the quadrant OPQ
$=\frac{1}{4}$ of the circle having radius OP
$=\frac{1}{4} \pi \mathrm{r}^{2}$
$=\frac{1}{4} \times \frac{22}{7} \times 21 \times 21$
$=346.5 \mathrm{~m}^{2}$
Total area of the field $=70 \times 52=3640 \mathrm{~m}^{2}$
Area left ungrazed = Area of the field - Area of the grazed field
$=3640-346.5=3293.5 \mathrm{~m}^{2}$
