Question:
A hemispherical bowl of internal radius 15 cm contains a liquid. The liquid is to be filled into cylindrical-shaped bottles of diameter 5 cm and height 6 cm. How many bottles are necessary to empty the bowl?
Solution:
Internal radius of hemispherical bowl r = 15 cm
The volume of bowl $=\frac{2}{3} \pi r^{3}=$ volume of liquid $=\frac{2}{3} \pi(15)^{3}$
Volume of liquid $=2250 \pi \mathrm{cm}^{3}$
Since, the liquid filled into the cylindrical shaped bottles of radius $\frac{5}{2} \mathrm{~cm}$ and height $6 \mathrm{~cm}$.
Let n be the no. of bottles.
Therefore,
The volume of liquid = n × volume of cylindrical shaped bottle
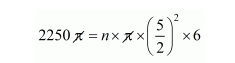
$2250=n \times \frac{25}{4} \times 6$
$n=\frac{2250 \times 4}{25 \times 6}$
$=60$
$n=60$
Hence, the no. of bottles = 60
