Question:
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Solution:
Radius of hemisphere r = 7 cm
The volume of hemisphere
$=\frac{2}{3} \pi r^{3}$
$=\frac{2}{3} \pi \times(7)^{3}$
$=\frac{2}{3} \pi \times 343$
$=\frac{686}{3} \pi \mathrm{cm}^{3}$
Since, the hemisphere cast into the right circular cone
The height of cone h = 49 cm
Let x be the radius of cone.
Clearly,
Volume of cone = volume of hemisphere
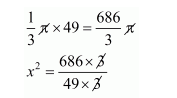
$=14$
$x^{2}=14$
$x=\sqrt{14}$
$x=3.74 \mathrm{~cm}$
Thus, the radius of cone = 3.74 cm
