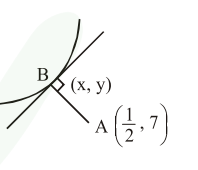
A helicopter is flying along the curve given by $y-x^{3 / 2}=7,(x \geq 0)$. A soldier positioned at the
$\operatorname{point}\left(\frac{1}{2}, 7\right)$ wants to shoot down the helicopter
when it is nearest to him. Then this nearest distance is :
Correct Option: , 3
$y-x^{3 / 2}=7(x \geq 0)$
$\frac{d y}{d x}=\frac{3}{2} x^{1 / 2}$
$\left(\frac{3}{2} \sqrt{x}\right)\left(\frac{7-y}{\frac{1}{2}-x}\right)=-1$
$\left(\frac{3}{2} \sqrt{x}\right)\left(\frac{-x^{3 / 2}}{\frac{1}{2}-x}\right)=-1$
$\frac{3}{2} \cdot x^{2}=\frac{1}{2}-x$
$3 x^{2}=1-2 x$
$3 x^{2}+2 x-1=0$
$3 x^{2}+3 x-x-1=0$
$(x+1)(3 x-1)=0$
$\therefore \quad x=-1($ rejected $)$
$x=\frac{1}{3}$
$y=7+x^{3 / 2}=7+\left(\frac{1}{3}\right)^{3 / 2}$
$\ell_{\mathrm{AB}}=\sqrt{\left(\frac{1}{2}-\frac{1}{3}\right)^{2}+\left(\frac{1}{3}\right)^{3}}=\sqrt{\frac{1}{36}+\frac{1}{27}}$
$=\sqrt{\frac{3+4}{9 \times 12}}$
$=\sqrt{\frac{7}{108}}=\frac{1}{6} \sqrt{\frac{7}{3}}$
Option (3)
