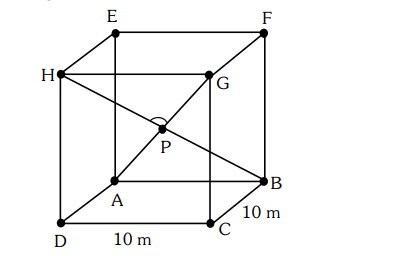
A hall has a square floor of dimension $10 \mathrm{~m} \times 10 \mathrm{~m}$ (see the figure) and vertical walls. If the angle GPH between the diagonals $\mathrm{AG}$ and $\mathrm{BH}$ is
$\cos ^{-1} \frac{1}{5}$, then the height of the hall (in meters) is :
Correct Option: , 4
$\mathrm{A}(\hat{\mathrm{j}}) \cdot \mathrm{B}(10 \hat{\mathrm{i}})$
$\mathbf{H}(\hat{\mathrm{h}}+10 \hat{\mathrm{k}})$
$\mathbf{G}(10 \hat{\mathrm{i}}+\mathrm{h} \hat{\mathrm{j}}+10 \hat{\mathrm{k}})$
$\overrightarrow{\mathrm{AG}}=10 \hat{\mathrm{i}}+\mathrm{h} \hat{\mathrm{j}}+10 \hat{\mathrm{k}}$
$\overrightarrow{\mathrm{BH}}=-10 \hat{\mathrm{i}}+\mathrm{h} \hat{\mathrm{j}}+10 \hat{\mathrm{k}}$
$\cos \theta=\frac{\overrightarrow{\mathrm{AG}} \overrightarrow{\mathrm{BH}}}{|\overrightarrow{\mathrm{AG}}||\overrightarrow{\mathrm{BH}}|}$
$\frac{1}{5}=\frac{h^{2}}{h^{2}+200}$
$4 \mathrm{~h}^{2}=200 \Rightarrow \mathrm{h}=5 \sqrt{2}$
