A force $\vec{F}=(\hat{i}+2 \hat{j}+3 \hat{k}) N$ acts at a point $(4 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-\hat{\mathrm{k}}) \mathrm{m}$. Then the magnitude of torque about the point $(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}}) \mathrm{m}$ will be $\sqrt{x}$ N-m. The value of $x$ is
$\vec{\tau}=\left(\overrightarrow{\mathrm{r}}_{2}-\overrightarrow{\mathrm{r}}_{1}\right) \times \overrightarrow{\mathrm{F}}$
$=[(4 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-\hat{\mathrm{k}})-(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}})] \times \overrightarrow{\mathrm{F}}$
$=(3 \hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}}) \times(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$
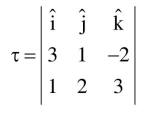
$=7 \hat{\mathrm{i}}-11 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}$
$|\vec{\tau}|=\sqrt{195}$
