A footpath of uniform width runs all around the inside of a rectangular field 54 m long and 35 m wide.

(i) Area of the rectangular field $=54 \times 35=1890 \mathrm{~m}^{2}$

Let the width of the path be x m. The path is shown in the following diagram:

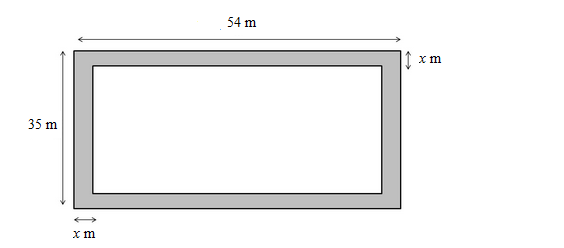
Length of the park excluding the path $=(54-2 x) \mathrm{m}$

Breadth of the park excluding the path $=(35-2 x) \mathrm{m}$

Thus, we have:
Area of the path = 420 m2

$\Rightarrow 420=54 \times 35-(54-2 x)(35-2 x)$

$\Rightarrow 420=1890-\left(1890-70 x-108 x+4 x^{2}\right)$

$\Rightarrow 420=-4 x^{2}+178 x$

$\Rightarrow 4 x^{2}-178 x+420=0$

$\Rightarrow 2 x^{2}-89 x+210=0$

$\Rightarrow 2 \mathrm{x}^{2}-84 \mathrm{x}-5 \mathrm{x}+210=0$

$\Rightarrow 2 \mathrm{x}(\mathrm{x}-42)-5(\mathrm{x}-42)=0$

$\Rightarrow(\mathrm{x}-42)(2 x-5)=0$

$\Rightarrow x-42=0$ or $2 x-5=0$

$\Rightarrow x=42$ or $\mathrm{x}=2.5$

The width of the path cannot be more than the breadth of the rectangular field.
∴ x = 2.5 m

​Thus, the path is 2.5 m wide.

(ii) Let the width of the border be x m.
The length and breadth of the carpet are 8 m and 5 m, respectively.

Area of the carpet $=8 \times 5=40 \mathrm{~m}^{2}$

Length of the carpet without border $=(8-2 x)$

Breadth of carpet without border $=(5-2 x)$

Area of the border = 12 m2

Area of the carpet without border $=(8-2 x)(5-2 x)$

Thus, we have:

$12=40-[(8-2 x)(5-2 x)]$

$\Rightarrow 12=40-\left(40-26 x+4 x^{2}\right)$

$\Rightarrow 12=26 x-4 x^{2}$

$\Rightarrow 26 x-4 x^{2}=12$

$\Rightarrow 4 x^{2}-26 x+12=0$

$\Rightarrow 2 x^{2}-13 x+6=0$

$\Rightarrow(2 x-1)(x-6)=0$

$\Rightarrow 2 x-1=0$ and $x-6=0$

$\Rightarrow x=\frac{1}{2}$ and $x=6$

Because the border cannot be wider than the entire carpet, the width of the carpet is $\frac{1}{2} \mathrm{~m}$, i.e., $50 \mathrm{~cm}$.