A flag-staff stands on the top of a 5 m high tower.

Let  be the tower height of m. flag height is m and an angle of elevation of top of tower is 45° and an angle of elevation of the top of flag is 60°.

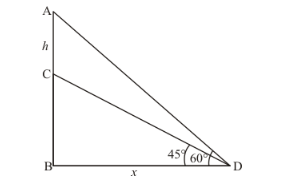
Let, $A C=h \mathrm{~m}$ and $B C=5 \mathrm{~m}$ and $\angle A D B=60^{\circ}, \angle C D B=45^{\circ}$

We have the corresponding angle as follows

'

So we use trigonometric ratios.

In a triangle,

$\Rightarrow \quad \tan 45^{\circ}=\frac{B C}{B D}$

$\Rightarrow \quad 1=\frac{5}{x}$

$\Rightarrow \quad x=5$

Again in a triangle $A B D$,

$\Rightarrow \quad \tan 60^{\circ}=\frac{A B}{B D}$

$\Rightarrow \quad \sqrt{3}=\frac{5+h}{5}$

$\Rightarrow \quad h=5(\sqrt{3}-1)$

$\Rightarrow \quad h=3.66$

Hence the height of flag is $3.66 \mathrm{~m}$.