A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m.

Solution:



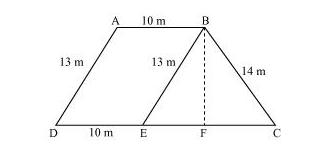
Draw a line BE parallel to AD and draw a perpendicular BF on CD.

It can be observed that ABED is a parallelogram.

BE = AD = 13 m

ED = AB = 10 m

EC = 25 − ED = 15 m

For $\triangle B E C$,

Semi-perimeter, $s=\frac{(13+14+15) \mathrm{m}}{2}=21 \mathrm{~m}$

By Heron’s formula,

Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$

Area of $\triangle B E C=[\sqrt{21(21-13)(21-14)(21-15)}] \mathrm{m}^{2}$

$=[\sqrt{21(8)(7)(6)}] \mathrm{m}^{2}=84 \mathrm{~m}^{2}$

Area of $\triangle B E C=\frac{1}{2} \times C E \times B F$

$\Rightarrow 84=\frac{1}{2} \times 15 \times \mathrm{BF}$

$\Rightarrow \mathrm{BF}=\frac{168}{15}=11.2 \mathrm{~m}$

Area of $A B E D=B F \times D E=11.2 \times 10=112 \mathrm{~m}^{2}$

Area of the field $=84+112=196 \mathrm{~m}^{2}$