A field is in the shape of a trapezium

In trapezium ABCD, we draw a perpendicular line CE to the line AB.

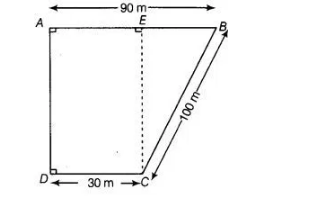
We have, $D C=A E=30 \mathrm{~m}$

Now, $\quad B E=A B-A E=90-30=60 \mathrm{~m}$

In right angled $\triangle B E C$, $(B C)^{2}=(B E)^{2}+(E C)^{2} \quad$ [using Pythagoras theorem]

$\Rightarrow \quad(100)^{2}=(60)^{2}+(E C)^{2}$

$\Rightarrow \quad(E C)^{2}=10000-3600$

$\Rightarrow \quad(E C)^{2}=6400$

$\therefore \quad E C=\sqrt{6400}=80 \mathrm{~m}$

[taking positive square root because length is always positive]

$\therefore \quad$ Area of trapezium $A B C D=\frac{1}{2}$ (Sum of parallel sides) $\times$ Distance between parallel sides

$\therefore \quad$ Area of trapezium $A B C D=\frac{1}{2}$ (Sum of parallel sides) $\times$ Distance between parallel sides

$=\frac{1}{2}(A B+C D) \times E C=\frac{1}{2}(90+30) \times 80$

$=\frac{1}{2} \times(120) \times 80=4800 \mathrm{~m}^{2}$

$\because$ Cost of ploughing the field of $1 \mathrm{~m}^{2}=₹ 4$

$\therefore$ Cost of ploughing the field of $4800 \mathrm{~m}^{2}=4800 \times 4=₹ 19200$

Hence, the total cost of ploughing the field is $₹ 19200$.