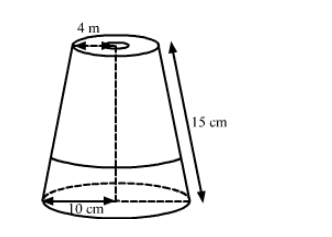
A fez, the cap used by the Turks, is shaped like the frustum of a cone.

We have,

Radius of open side, $R=10 \mathrm{~cm}$,

Radius of upper base, $r=4 \mathrm{~cm}$ and

Slant height, $l=15 \mathrm{~cm}$

Now,

The area of material used $=\pi(R+r) l+\pi r^{2}$

$=\frac{22}{7} \times(10+4) \times 15+\frac{22}{7} \times 4 \times 4$

$=\frac{22}{7} \times 14 \times 15+\frac{22}{7} \times 4 \times 4$

$=\frac{22}{7} \times(14 \times 15+4 \times 4)$

$=\frac{22}{7} \times(210+16)$

$=\frac{22}{7} \times 226$

$=\frac{4972}{7} \mathrm{~cm}^{2}$

$\approx 710.28 \mathrm{~cm}^{2}$

So, the area of material used for making the fez is 710.28 cm2.