A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A,
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin content of one kg food is given below:
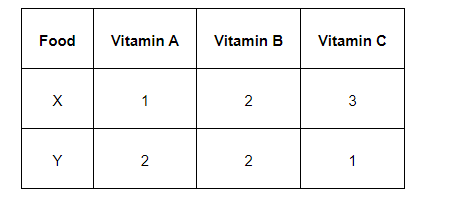
One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?
Let the mixture contain x kg of food X and y kg of food Y.
The mathematical formulation of the given problem is as follows.
Minimize $z=16 x+20 y$ (1)
subject to the constraints,
$x+2 y \geq 10$ (2)
$x+y \geq 6$ (3)
$3 x+y \geq 8$ (4)
$x, y \geq 0$ (5)
The feasible region determined by the system of constraints is as follows.
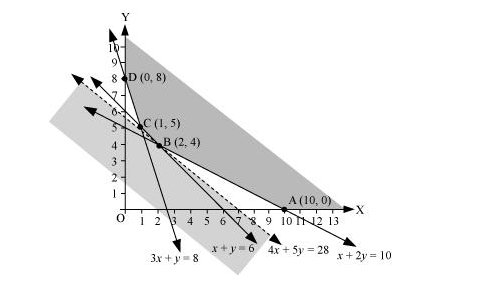
The corner points of the feasible region are A (10, 0), B (2, 4), C (1, 5), and D (0, 8).
The values of z at these corner points are as follows.

As the feasible region is unbounded, therefore, 112 may or may not be the minimum value of z.
For this, we draw a graph of the inequality, $16 x+20 y<112$ or $4 x+5 y<28$, and check whether the resulting half plane has points in common with the feasible region or not.
It can be seen that the feasible region has no common point with 4x + 5y < 28
Therefore, the minimum value of z is 112 at (2, 4).
Thus, the mixture should contain 2 kg of food X and 4 kg of food Y. The minimum cost of the mixture is Rs 112.
