Question:
A cylindrical vessel 32 cm high and 18 cm as the radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, the radius of its base is
(a) 12 cm
(b) 24 cm
(c) 36 cm
(c) 48 cm
Solution:
Volume of sand filled in cylindrical vessel
$=\pi(18)^{2} \times 32$
$=32 \times 324 \pi$
Clearly,
The volume of conical heap = volume of sand
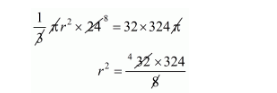
$r=\sqrt{4 \times 324}$
$r=2 \times 18$
$=36$
$r=36 \mathrm{~cm}$
Hence, the correct answer is choice (c).
