A cylindrical container is filled with ice-cream, whose diameter is 12 cm and height is 15 cm. the whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice-cream.
Volume of cylindrical container
$=\pi r^{2} h$
$=\pi \times(6)^{2} \times 15$
Amount of ice-cream distributed to 10 children $=\frac{\pi \times(6)^{2} \times 15}{10}$
Therefore,
Height of conical portion = 2 × diameter of its bars
Let the diameter of bare = r
Height = 2r
Therefore,
Volume of the cones
$=\frac{1}{3} \pi\left(\frac{r}{2}\right)^{2} h+\frac{2}{3} \pi r^{3}$
$=\frac{1}{3} \pi\left(\frac{r}{2}\right)^{2}(h+2 r)$
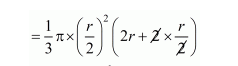
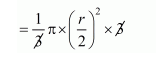
$r=\frac{\pi r^{3}}{4}$
Therefore,
Volume of the cones = amount distributed
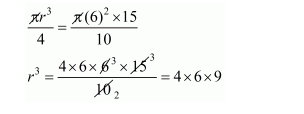
$r=\sqrt[3]{6 \times 6 \times 6}=6 \mathrm{~cm}$
