A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand.

For the cylindrical bucket :

Radius (r) = 18 cm and height (h) = 32 cm

Volume $=\pi \mathrm{r}^{2} \mathrm{~h}=\frac{\mathbf{2 2}}{\mathbf{7}}(18)^{2} \times 32 \mathrm{~cm}^{3}$

$\Rightarrow$ Volume of the sand $=\left(\frac{22}{7} \times 18 \times 18 \times 32\right) \mathrm{cm}^{3}$

For the conical heap :

Height (H) = 24 cm & let radius of the base be (R).

$\therefore$ Volume of conical heap

$=\frac{1}{3} \pi R^{2} \mathbf{H}=\left[\frac{1}{3} \times \frac{22}{7} \times \mathbf{R}^{2} \times 24\right] \mathrm{cm}^{3}$

$\because$ Volume of conical heap sand $=$ Volume of the sand

$\therefore \frac{\mathbf{1}}{\mathbf{3}} \times \frac{\mathbf{2 2}}{\mathbf{7}} \times \mathbf{R}^{\mathbf{2}} \times \mathbf{2 4}=\frac{\mathbf{2 2}}{\mathbf{7}} \times 18 \times 18 \times 32$

$\Rightarrow \mathrm{R}^{2}=\frac{\mathbf{1 8} \times \mathbf{1 8} \times \mathbf{3 2} \times \mathbf{3}}{\mathbf{2 4}}=18^{2} \times 2^{2}$

$\Rightarrow \mathrm{R}=\sqrt{\mathbf{1 8}^{2} \times \mathbf{2}^{2}}=18 \times 2 \mathrm{~cm}=36 \mathrm{~cm}$

Let ' $\ell$ ' be the slant height of the conical heap of the sand.

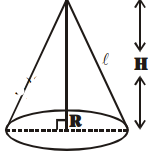
$\therefore \quad \ell^{2}=\mathrm{H}^{2}+\mathrm{R}^{2}$

$\Rightarrow \ell^{2}=24^{2}+36^{2}$

$\Rightarrow \ell^{2}=(12 \times 2)^{2}+(12 \times 3 )^{2}$

$\Rightarrow \ell^{2}=12^{2}\left[2^{2}+3^{2}\right]$

$\Rightarrow \ell^{2}=12^{2} \times 13$

$\Rightarrow \ell=\sqrt{12^{2} \times 13}=12 \times \sqrt{13}$

Thus, the required radius $=36 \mathrm{~cm}$ and slant height $=\mathbf{1 2} \sqrt{\mathbf{1 3}} \mathrm{cm}$