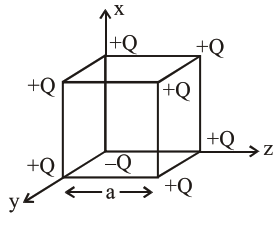
A cube of side 'a' has point charges $+Q$ located at each of its vertices except at the origin where the charge is $-\mathrm{Q}$. The electric field at the centre of cube is :
Correct Option: , 2
We can replace $-Q$ charge at origin by $+Q$ and $-2 Q$. Now due to $+Q$ charge at every corner of cube. Electric field at center of cube is zero so now net electric field at center is only due to $-2 \mathrm{Q}$ charge at origin.
$\overrightarrow{\mathrm{E}}=\frac{\mathrm{kq} \overrightarrow{\mathrm{r}}}{\mathrm{r}^{3}}=\frac{1(-2 \mathrm{Q}) \frac{\mathrm{a}}{2}(\hat{\mathrm{x}}+\hat{\mathrm{y}}+\hat{\mathrm{z}})}{4 \pi \varepsilon_{0}\left(\frac{\mathrm{a}}{2} \sqrt{3}\right)^{3}}$
$\overrightarrow{\mathrm{E}}=\frac{-2 \mathrm{Q}(\hat{\mathrm{x}}+\hat{\mathrm{y}}+\hat{\mathrm{z}})}{3 \sqrt{3} \pi \mathrm{a}^{2} \varepsilon_{0}}$
