Question:
A cord is wound round the circumference of wheel of radius $\mathbf{r}$. The axis of the wheel is horizontal and the moment of inertia about it is I. A weight $\mathrm{mg}$ is attached to the cord at the end. The weight falls from rest. After falling through a distance 'h', the square of angular velocity of wheel will be:
Correct Option: , 4
Solution:
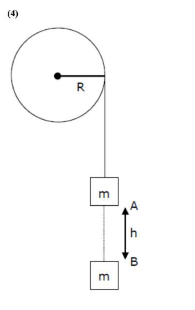
using energy conservation between $\mathrm{A}$ and $\mathrm{B}$ point
$m g h=\frac{1}{2} m(w R)^{2}+\frac{1}{2} I \omega^{2}$
$2 \mathrm{mgh}=\left(\mathrm{MR}^{2}+\mathrm{I}\right) \omega^{2}$
$\omega^{2}=\frac{2 m g h}{I+M R^{2}}$
