Question:
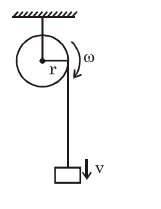
A cord is wound round the circumference of wheel of radius $\mathrm{r}$. The axis of the wheel is horizontal and the moment of inertia about it is I. A weight $\mathrm{mg}$ is attached to the cord at the end. The weight falls from rest. After falling through a distance ' $h$ ', the square of angular velocity of wheel will be :-
Correct Option: , 3
Solution:
$m g h=\frac{1}{2} I \omega^{2}+\frac{1}{2} m v^{2}$
$\mathrm{v}=\omega \mathrm{\omega r}$
$\mathrm{mgh}=\frac{1}{2} \mathrm{I} \omega^{2}+\frac{1}{2} \mathrm{~m} \omega^{2} \mathrm{r}^{2}$
$\frac{2 m g h}{\left(I+m r^{2}\right)}=\omega^{2}$