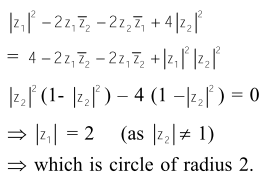Question:
A complex number $z$ is said to be unimodular if $|z|=1$. Suppose $z_{1}$ and $z_{2}$ are complex numbers such that $\frac{z_{1}-2 z_{2}}{2-z_{1} \bar{z}_{2}}$ is unimodular and $z_{2}$ is not unimodular. Then the point $z_{1}$ lies on a :
Correct Option: 1
Solution: