Question:
A coil having $N$ turns is wound tightly in the form of a spiral with inner and outer radii 'a' and 'b' respectively. Find the magnetic field at centre, when a current I passes through coil:
Correct Option: 1
Solution:
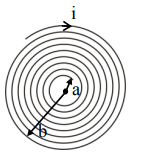
No. of turns in $\mathrm{dx}$ width $=\frac{\mathrm{N}}{\mathrm{b}-\mathrm{a}} \mathrm{dx}$
$\int d B=\int_{a}^{b}\left(\frac{N}{b-a}\right) d x \frac{\mu_{0} i}{2 x}$
$\mathrm{B}=\frac{\mathrm{N} \mu_{0} \mathrm{i}}{2(\mathrm{~b}-\mathrm{a})} \ell \mathrm{n}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)$
Option (1)
