Question:
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent.
Solution:
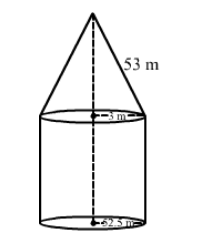
Radius of the cylinder = 52.5 m
Radius of the base of the cone = 52.5 m
Slant height (l) of the cone = 53 m
Height of the cylinder (h) = 3 m
Curved surface area of the cylindrical portion $=2 \pi r h=\left(2 \times \frac{22}{7} \times 52.5 \times 3\right) \mathrm{m}^{2}=990 \mathrm{~m}^{2}$
Curved surface area of the conical portion $=\pi r l=\left(\frac{22}{7} \times 52.5 \times 53\right) \mathrm{m}^{2}=8745 \mathrm{~m}^{2}$
Thus, the total area of canvas required for making the tent $=(8745+990) \mathrm{m}^{2}=9735 \mathrm{~m}^{2}$
