A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground
Question:
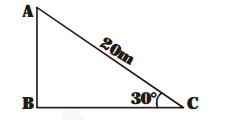
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30° (see fig.).
Solution:
AC = 20 m is the length of the rope.
Let AB = h metres be the height of the pole
$\angle \mathrm{ACB}=30^{\circ}($ Given $)$
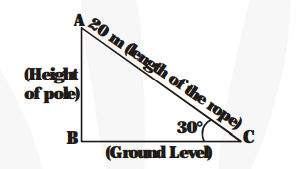
Now, $\frac{\mathbf{A B}}{\mathbf{A C}}=\sin \mathbf{3 0}^{\circ}=\frac{\mathbf{1}}{\mathbf{2}}$
$\frac{h}{20}=\frac{1}{2}$
$h=10 \mathrm{~m}$
