A circular hole of radius $\left(\frac{2}{2}\right)$ is cut out of a circular dise of radius 'a' shown in ligure. The centroid of the remaining circular portion with respect to point ' $\mathrm{O}^{\prime}$ will be :
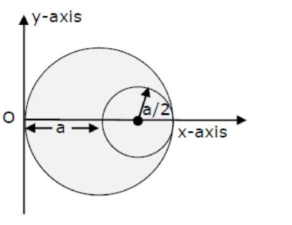
Correct Option: , 4
(4)
Let $\sigma$ is the surface mass density of disc.
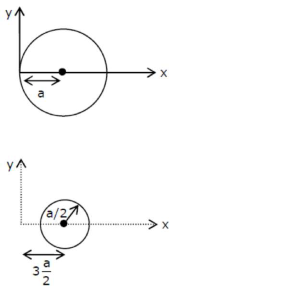
$X_{\mathrm{com}}=\frac{\left(0 \times \pi a^{2} \times A\right)-\left(\frac{\pi^{2}}{\frac{1}{4}} \times \frac{3 \pi}{2}\right)}{\sigma \pi a^{2}-\frac{m^{2}}{4}}$
$\mathrm{X}_{\text {enn }}=\frac{a-3 \frac{4}{5}}{1-\frac{1}{4}}$
$X_{\text {enm }}=\frac{\frac{\mathrm{k}}{\frac{3}{3}}}{\frac{3}{4}}$
$X_{\text {enm }}=\frac{5_{0}}{6}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.