A circular field has a perimeter of 650 m.

We have a circular field in which a square field is marked.

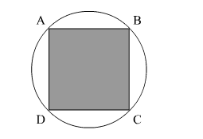
Let the radius of the circle be r. We have,

Perimeter $=650$

$r=\frac{325}{\pi}$

Use Pythagoras theorem to find the side of square as,

$\mathrm{AB}=\sqrt{r^{2}+r^{2}}$

$=\frac{325}{\pi} \sqrt{2}$

So area of the square plot,

$=(\mathrm{AB})^{2}$

$=\left(\frac{325}{\pi} \sqrt{2}\right)^{2} \mathrm{~m}^{2}$

$=\left(\frac{325(7)}{22} \sqrt{2}\right)^{2} \mathrm{~m}^{2}$

$=21387 \mathrm{~m}^{2}$