A circle has radius √2 cm.

Draw a circle having centre $O$. Let $A B=2 \mathrm{~cm}$ be a chord of a circle. A chord $A B$ is divided by the line OM in two equal segments.

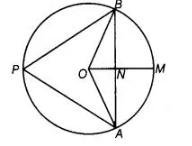
To prove $\angle A P B=45^{\circ}$

Here, $\quad A N=N B=1 \mathrm{~cm}$

and $O B=\sqrt{2} \mathrm{~cm}$

In $\triangle O N B$, $O B^{2}=O N^{2}+N B^{2}$

[use Pythagoras theorem]

$\Rightarrow \quad(\sqrt{2})^{2}=O N^{2}+(1)^{2}$

$\Rightarrow \quad O N^{2}=2-1=1$

$\Rightarrow \quad O N=1 \mathrm{~cm}$

[taking positive square root, because distance is always positive]

Also, $\angle O N B=90^{\circ}$ [ON is the perpendicular bisector of the chord $A B$ ]

$\therefore$ $\angle N O B=\angle N B O=45^{\circ}$

Similarly, $\angle A O N=45^{\circ}$

Now, $\angle A O B=\angle A O N+\angle N O B$

$=45^{\circ}+45^{\circ}=90^{\circ}$

We know that, chord subtends an angle to the circle is half the angle subtended by it to the centre.

$\therefore$ $\angle A P B=\frac{1}{2} \angle A O B$

$=\frac{90^{\circ}}{2}=45^{\circ}$ 

Hence proved.