A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle.

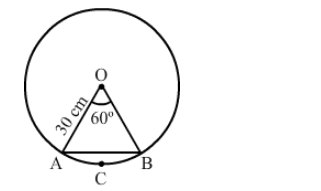
Let $A B$ be the chord of a circle with centre $O$ and radius $30 \mathrm{~cm}$ such that $\angle A O B=60^{\circ}$.

Area of the sector $O A C B O=\frac{\pi r^{2} \theta}{360}$

$=\left(3.14 \times 30 \times 30 \times \frac{60}{360}\right) \mathrm{cm}^{2}$

$=471 \mathrm{~cm}^{2}$

Area of $\Delta O A B=\frac{1}{2} r^{2} \sin \theta$

$=\left(\frac{1}{2} \times 30 \times 30 \times \sin 60^{\circ}\right) \mathrm{cm}^{2}$

$=(225 \times 1.732) \mathrm{cm}^{2}$

$=389.7 \mathrm{~cm}^{2}$

Area of the minor segment $=($ Area of the sector $O A C B O)-($ Area of $\Delta O A B)$

$=(471-389.7) \mathrm{cm}^{2}$

$=81.3 \mathrm{~cm}^{2}$

Area of the major segment $=$ (Area of the circle) $-$ (Area of the minor segment)

$=|(3.14 \times 30 \times 30)-81.3| \mathrm{cm}^{2}$

$=2744.7 \mathrm{~cm}^{2}$