A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle.

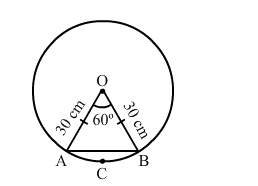
Let the chord be AB. The ends of the chord are connected to the centre of the circle O to give the triangle OAB.

OAB is an isosceles triangle. The angle at the centre is 60

Area of the triangle $=\frac{1}{2}(30)^{2} \sin 60^{\circ}=450 \times \frac{\sqrt{3}}{2}=389.25 \mathrm{~cm}^{2}$

Area of the sector $O A C B O=\frac{60}{360} \times \pi \times 30 \times 30=150 \pi=471 \mathrm{~cm}^{2}$

Area of the minor segment $=$ Area of the sector $-$ Area of the triangle

$=471-389.25=81.75 \mathrm{~cm}^{2}$

Area of the major segment = Area of the circle - Area of the minor segment

$=(\pi \times 30 \times 30)-81.29$

$=2744.71 \mathrm{~cm}^{2}$