A chord of a circle is equal to its radius.

Given, AB is a chord of a circle, which is equal to the radius of the circle, i.e.,

AB = BO …(i)

Join OA, AC and BC.

Since, OA = OB= Radius of circle

OA = AS = BO

Thus, $\triangle O A B$ is an equilateral triangle.

$\Rightarrow \quad \angle A O B=60^{\circ} \quad$ [each angle of an equilateral triangle is $60^{\circ}$ ]

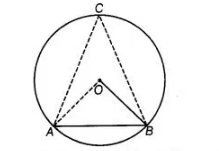
By using the theorem, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

i.e., $\angle \mathrm{AOB}=2 \angle \mathrm{ACB}$

$\Rightarrow \quad \angle A C B=\frac{60^{\circ}}{2}=30^{\circ}$