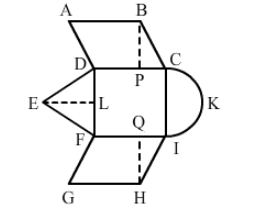
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
CD = 8 cm
BP = HQ = 4 cm
DE = EF = 5 cm
Area of the parallelogram $\mathrm{ABCD}=B \times H$
$=8 \times 4$
$=32$ sq. $\mathrm{cm}$
Area of parallelogram $\mathrm{FGHI}=B \times H$
$=8 \times 4$
$=32$ sq. $\mathrm{cm}$
Area of the square $=\operatorname{Side}^{2}$
$=8^{2}=64$ sq. $\mathrm{cm}$
In $\Delta \mathrm{ELF}$, we have:
$\mathrm{EL}^{2}=5^{2}-4^{2}$
$\mathrm{EL}^{2}=9$
$\mathrm{EL}=3 \mathrm{~cm}$
Area of $\triangle \mathrm{DEF}=\frac{1}{2} \times B \times H$
$=\frac{1}{2} \times 8 \times 3$
$=12$ sq. $\mathrm{cm}$
Area of the semicircle $=\frac{1}{2} \pi r^{2}$
$=\frac{1}{2} \times \frac{22}{7} \times 16$
$=25.12$ sq. $\mathrm{cm}$
∴ Total Area = Area of the parallelogram ABCD + Area of the parallelogram FGHI + Area of the triangle DEF + Area of the semicircle CKI + Area of the square
Total Area = 165.12 cm2
