A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m

Let the length of stool,m, height m and its leg inclined at an angle ofto the ground.

Let length of leg $A E=h \mathrm{~m}$.

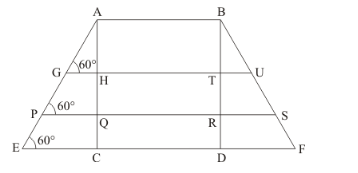
We have to find length of leg, lengths of two steps equal in length.

$\ln _{\triangle A E C}, \angle A E C=60^{\circ}$

$\sin 60^{\circ}=\frac{A C}{A E}$

$\Rightarrow \frac{\sqrt{3}}{2}=\frac{1.5}{h}$

$\Rightarrow h=\frac{3}{\sqrt{3}}$

$\Rightarrow h=1.732$

In $\triangle A G H, \angle A G H=60^{\circ}$ and $A H=0.5 \mathrm{~m}$

$\tan 60^{\circ}=\frac{A H}{G H}$

$\Rightarrow \sqrt{3}=\frac{0.5}{G H}$

$\Rightarrow G H=\frac{0.5}{\sqrt{3}}$

$\Rightarrow G H=0.2886$

Total length $=0.5+(0.2886 \times 2)=1.1077 \mathrm{~m}$.

In $\triangle A P Q, \angle A P Q=60^{\circ}$ and $A Q=1 \mathrm{~m}$

$\tan 60^{\circ}=\frac{A Q}{P Q}$

$\Rightarrow \sqrt{3}=\frac{1}{P Q}$

$\Rightarrow P Q=\frac{1}{\sqrt{3}}$

$\Rightarrow P Q=0.577$

Total lengths $0.5+(0.577 \times 2)=1.654 \mathrm{~m}$

Hence the length of leg is $1.732 \mathrm{~m}$.

And lengths of each step are $1.1077 \mathrm{~m}$ and $1.654 \mathrm{~m}$.