Question:
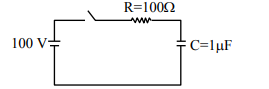
A capacitor of capacitance $\mathrm{C}=1 \mu \mathrm{F}$ is suddenly connected to a battery of 100 volt through a resistance $R=100 \Omega$. The time taken for the capacitor to be charged to get $50 \mathrm{~V}$ is :
$[$ Take $\ln 2=0.69]$
Correct Option: , 3
Solution:
$\mathrm{V}=\mathrm{V}_{0}\left(1-\mathrm{e}^{-\frac{\mathrm{t}}{R C}}\right)$
$50=100\left(1-e^{-\frac{t}{R C}}\right)$
$\mathrm{t}=0.69 \times 10^{-4} \mathrm{sec}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.