Question:
A bullet of $10 \mathrm{~g}$, moving with velocity $v$, collides head-on with the stationary bob of a pendulum and recoils with velocity $100 \mathrm{~m} / \mathrm{s}$. The length of the pendulum is $0.5 \mathrm{~m}$ and mass of the bob is $1 \mathrm{~kg}$. The minimum value of $v=$ $\mathrm{m} / \mathrm{s}$ so that the pendulum describes a circle. (Assume the string to be inextensible and $g=10 \mathrm{~m} / \mathrm{s}^{2}$ )
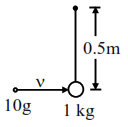
Solution:
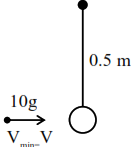
$V^{\prime}=\sqrt{5 \mathrm{gR}}=\sqrt{5 \times 10 \times 0.5}$
$\mathrm{V}^{\prime}=5 \mathrm{~m} / \mathrm{s}$
$\mathrm{m}_{\mathrm{l}} \mathrm{V}=\mathrm{m}_{2} \times 5-\mathrm{m}_{\mathrm{l}} \times 100$
$\frac{10}{1000} \times V=5-\frac{10}{1000} \times 100$
$\mathrm{V}=400 \mathrm{~m} / \mathrm{s}$
