A box open from top is made from a rectangular sheet of dimension $\mathrm{a} \times \mathrm{b}$ by cutting squares each of side $x$ from each of the four corners and folding up the flaps. If the volume of the box is maximum, then $\mathrm{x}$ is equal to :
Correct Option: , 3
$\mathrm{V}=\ell . \mathrm{b} . \mathrm{h}=(\mathrm{a}-2 \mathrm{x})(\mathrm{b}-2 \mathrm{x}) \mathrm{x}$
$\Rightarrow \mathrm{V}(\mathrm{x})=(2 \mathrm{x}-\mathrm{a})(2 \mathrm{x}-\mathrm{b}) \mathrm{x}$
$\Rightarrow \mathrm{V}(\mathrm{x})=4 \mathrm{x}^{3}-2(\mathrm{a}+\mathrm{b}) \mathrm{x}^{2}+\mathrm{abx}$
$\Rightarrow \frac{\mathrm{d}}{\mathrm{dx}} \mathrm{v}(\mathrm{x})=12 \mathrm{x}^{2}-4(\mathrm{a}+\mathrm{b}) \mathrm{x}+\mathrm{ab}$
$\frac{\mathrm{d}}{\mathrm{dx}}(\mathrm{v}(\mathrm{x}))=0 \Rightarrow 12 \mathrm{x}^{2}-4(\mathrm{a}+\mathrm{b}) \mathrm{x}+\mathrm{ab}=0<_{\beta}^{\alpha}$
$\Rightarrow x=\frac{4(a+b) \pm \sqrt{16(a+b)^{2}-48 a b}}{2(12)}$
$=\frac{(\mathrm{a}+\mathrm{b}) \pm \sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}-\mathrm{ab}}}{6}$
Let $x=\alpha=\frac{(a+b)+\sqrt{a^{2}+b^{2}-a b}}{6}$
$\beta=\frac{(a+b)-\sqrt{a^{2}+b^{2}-a b}}{6}$
Now, $12(x-\alpha)(x-\beta)=0$
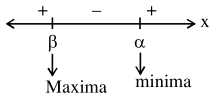
$\therefore \quad x=\beta$
$=\frac{a+b-\sqrt{a^{2}+b^{2}-a b}}{b}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.